Magical Elements
Inductor
An inductor, also called a coil or reactor, is a passive two-terminal electrical component which resists changes inelectric current passing through it. It consists of a conductor such as a wire, usually wound into a coil. Energy is stored in a magnetic field in the coil as long as current flows. When the current flowing through an inductor changes, the time-varying magnetic field induces a voltage in the conductor, according to Faraday’s law of electromagnetic induction.
Lenz law-
Lenz's law states that when an emf is generated by a change in magnetic flux according to Faraday's Law, the polarity of the induced emf is such, that it produces an current that's magnetic field opposes the change which produces it.
Inductor
Definition of Inductance
If a changing flux is linked with a coil of a conductor there would be an emf induced in it. The property of the coil of inducing emf due to the changing flux linked with it is known as inductance of the coil. Due to this property all electrical coil can be referred as inductor. In other way, an inductor can be defined as an energy storage device which stores energy in form of magnetic field.
An inductor, also called a coil or reactor, is a passive two-terminal electrical component which resists changes inelectric current passing through it. It consists of a conductor such as a wire, usually wound into a coil. Energy is stored in a magnetic field in the coil as long as current flows. When the current flowing through an inductor changes, the time-varying magnetic field induces a voltage in the conductor, according to Faraday’s law of electromagnetic induction.
Lenz's law states that when an emf is generated by a change in magnetic flux according to Faraday's Law, the polarity of the induced emf is such, that it produces an current that's magnetic field opposes the change which produces it.
The negative sign used in Faraday's law of electromagnetic induction, indicates that the induced emf ( ε ) and the change in magnetic flux ( δΦB ) have opposite signs.
Where,
ε = Induced emf
δΦB = change in magnetic flux
N = No of turns in coil
Where,
ε = Induced emf
δΦB = change in magnetic flux
N = No of turns in coilExplanation of Lenz's Law
For understanding Lenz's law, consider two cases :
CASE-I When a magnet is moving towards the coil.
When the north pole of the magnet is approaching towards the coil, the magnetic flux linking to the coil increases. According to Faraday's law of electromagnetic induction, when there is change in flux, an emf and hence current is induced in the coil and this current will create its own magnetic field . Now according to Lenz's law, this magnetic field created will oppose its own or we can say opposes the increase in flux through the coil and this is possible only if approaching coil side attains north polarity, as we know similar poles repel each other. Once we know the magnetic polarity of the coil side, we can easily determine the direction of the induced current by applying right hand rule. In this case, the current flows in anticlockwise direction.
When the north pole of the magnet is approaching towards the coil, the magnetic flux linking to the coil increases. According to Faraday's law of electromagnetic induction, when there is change in flux, an emf and hence current is induced in the coil and this current will create its own magnetic field . Now according to Lenz's law, this magnetic field created will oppose its own or we can say opposes the increase in flux through the coil and this is possible only if approaching coil side attains north polarity, as we know similar poles repel each other. Once we know the magnetic polarity of the coil side, we can easily determine the direction of the induced current by applying right hand rule. In this case, the current flows in anticlockwise direction.
CASE-II When a magnet is moving away from the coil
When the north pole of the magnet is moving away from the coil, the magnetic flux linking to the coil decreases. According to Faraday's law of electromagnetic induction, an emf and hence current is induced in the coil and this current will create its own magnetic field . Now according to Lenz's law, this magnetic field created will oppose its own or we can say opposes the decrease in flux through the coil and this is possible only if approaching coil side attains south polarity, as we know dissimilar poles attract each other. Once we know the magnetic polarity of the coil side, we can easily determine the direction of the induced current by applying right hand rule. In this case, the current flows in clockwise direction.
When the north pole of the magnet is moving away from the coil, the magnetic flux linking to the coil decreases. According to Faraday's law of electromagnetic induction, an emf and hence current is induced in the coil and this current will create its own magnetic field . Now according to Lenz's law, this magnetic field created will oppose its own or we can say opposes the decrease in flux through the coil and this is possible only if approaching coil side attains south polarity, as we know dissimilar poles attract each other. Once we know the magnetic polarity of the coil side, we can easily determine the direction of the induced current by applying right hand rule. In this case, the current flows in clockwise direction.
NOTE : For finding the directions of magnetic field or current, use right hand thumb rule i.e if the fingers of the right hand are placed around the wire so that the thumb points in the direction of current flow, then the curling of fingers will show the direction of the magnetic field produced by the wire.
Properties of Inductors
|
The I-V law for a inductor is for the reference directions shown below.
 |
1) The voltage across an inductor is zero if the current through the inductor is not changing. i.e. Since di/dt=0 and v=Ldi/dt, then v=0v.
2) The current through an inductor cannot change instantaneously. i.e. If di/dt®¥, then v=Ldi/dt®¥ which is not possible. Therefore i cannot change instantaneously.
3) In a circuit with only DC sources, an inductor "acts like" a short-circuit after the current through it reaches steady-state. The energy stored is
 |
4) An inductor is a passive device that stores energy. The energy associated with the inductor is stored in the magnetic field surrounding the device. The energy can be completely recovered by "collapsing" this magnetic field. If discharged through a resistive device the power given off as heat will come from the magnetic field.
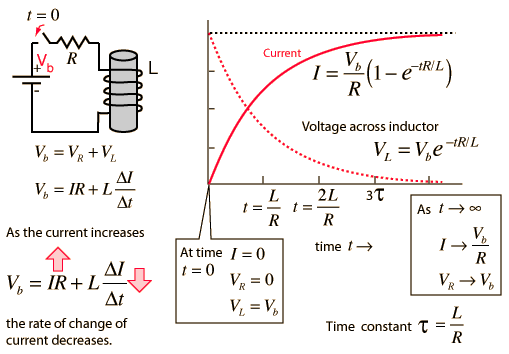
Inductor Transient
When a battery is connected to a series resistor and inductor, the inductor resists the change in current and the current therefore builds up slowly. Acting in accordance with Faraday's law and Lenz's law, the amount of impedance to the buildup of current is proportional to the rate of change of the current. That is, the faster you try to make it change, the more it resists. The current builds up toward the value it would have with the resistor alone because once the current is no longer changing, the inductor offers no impedance. The rate of this buildup is characterized by the time constant L/R . Establishing a current in an inductor stores energy in the magnetic field formed by the coils of the inductor.
No comments:
Post a Comment